初级篇¶

1 前文回顾¶

前文——《写给你的金融时间序列分析：基础篇》——介绍了金融时间序列的核心特性：自相关性；说明**金融时间序列分析的核心正是挖掘该时间序列中的自相关性**。一个优秀的模型应该能够有效的刻画原始时间序列中不同间隔的自相关性；而衡量一个模型是否适合原始时间序列的标准正是考察原始值和拟合值之间的残差序列是否近似的为白噪声。

本篇是系列的第二篇，初级篇。白噪声正是本文的内容之一，它是时间序列分析中最基本的模型。在它的基础上延伸出的另一个基本模型便是随机游走。通常，白噪声和随机游走被认为是用来分别描述投资品收益率和价格的最简单模型。我们稍后会看到，对于收益率来说（特别是股指的收益率），白噪声模型并不有效。

2 时间序列建模¶

本质上说讲，时间序列模型是一个可以“解释”时间序列中的自相关性的数学模型。

能够解释时间序列的自相关性在量化投资领域意义重大：

我们假设金融时间序列（比如投资品的收益率）存在未知的自相关性（当然也伴随着噪声），而这种自相关性体现了该时间序列某种内在的特性（比如趋势、或者均值回复），而这种内在特性是可以延续的（至少在未来短时间内）。因此，我们希望通过对历史数据的拟合找到一个合适的模型，使得它能最大程度的解释该时间序列表现出来的自相关性。基于未来会重复历史的假设，我们在统计上预期这种自相关性存在于未来的序列中，由于这个模型考虑了这种自相关性，因此它将会帮助我们来预测未来。

时间序列分析为我们研究投资品收益率的行为提供了有力的统计学框架

在投资中，对收益率的预测显然是非常有用的。如果我们能够预测投资品的涨跌，那么就能基于此构建一个交易策略；如果我们能够预测收益率的波动率，那么就可以进行风险管理（因此我们对时间序列的二阶统计量——如方差——同样感兴趣）。

假设原始时间序列为 $\{y_t\}$，模型拟合出来的序列为 $\{p_t\}$，则残差序列 $\{e_t\}$ 定义为原始序列和拟合序列的差值：

\[e_t = y_t - p_t \]

如果模型很好的捕捉了原始时间序列的自相关性，那么残差序列 $\{e_t\}$应该近似的为白噪声，对任何非零间隔 $k$，该残差序列的自相关系数 $\rho_k$ 都应该在统计意义上不显著的偏离 $0$。

当然，这仅仅是我们说该模型是个优秀模型的充分条件，因为一个好模型最关键的还是能产生赚钱的交易信号。因此，模型的检验最终还要看它在样本外预测的准确性

时间序列建模的过程可以总结如下：

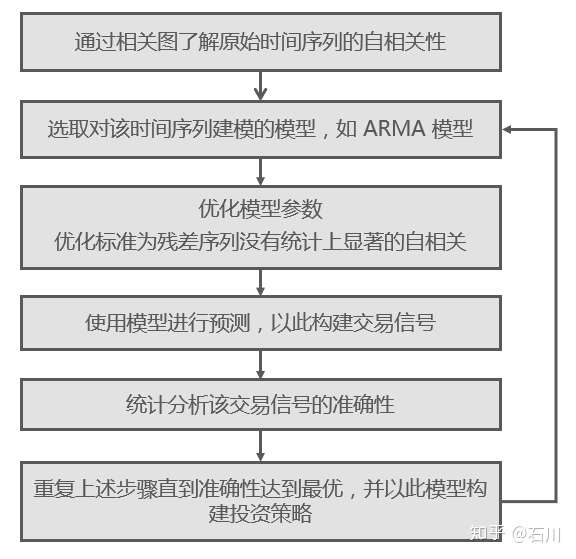
对于一个时间序列，我们总是希望首先画出它的相关图来看看它存在什么样的自相关性。基于对其自相关性的认知，第二步则是选择合适的模型，比如 AR、MA 或者 ARMA 模型，甚至于更高级对波动率建模的 GARCH 模型等。选定模型后，接下来便需要优化模型的参数，以使其尽可能解释时间序列的自相关性。在这一步，我们通过对残差进行自相关性分析来判断模型是否合适。在这方面，Ljung–Box 检验是一个很好的方法，它同时检验给残差序列各间隔的自相关系数是否显著的不为 0。在选定模型参数之后，仍需定量评价该模型在样本外预测的准确性。毕竟，对于样本内的数据，错误的**过拟合**总会得到“优秀”的模型，但它们往往对样本外数据的预测效果很差。因此，只有样本外预测的准确性才能客观的评价模型的好坏。如果模型的准确性较差，这说明该模型存在缺陷，无法充分捕捉原序列的自相关性。这时必须考虑更换模型。这就构成了上述步骤的反馈回路，直到最终找到一个既能解释原时间序列自相关性，又能在样本外有不错的准确性的模型。之后，该模型将被用来产生交易型号并构建量化投资策略。

接下来我们就来介绍一个最简单的时间序列模型：白噪声。

3. 白噪声¶

本文第一节指出，对于收益率来说，白噪声（white noise）**并不是一个十分有效的模型。那么为什么我们还要研究它呢？这是因为它有一个重要的特性，即**序列不相关：一个白噪声序列中的每一个点都独立的来自某个未知的分布，它们满足独立同分布（independent and identically distributed）。

一个（离散）白噪声的定义如下：

考虑时间序列 ({ w_t{}:{}t=1,\cdots,n } (。如果该序列的成分 $w_t$ 满足均值为\)0\)，方差 $\sigma^2$，且对于任意的 (k \ge 1 $，自相关系数$\rho_k\) 均为 $0$ ，则称该时间序列为一个离散的白噪声。

上面的定义并没有假设 $w_t$ 来自正态分布。事实上，白噪声对分布没有要求。当 $w_t$ 来自正态分布时，该序列又称为高斯白噪声（Gaussian white noise）。

根据白噪声的定义，一个白噪声序列显然满足平稳性要求。它的均值和二阶统计量为：

\[ \begin{align*} \mu_w & = & 0 \\ \rho_k & = & \begin{cases} 1 & \text{if } k = 0 \\ 0 & \text{if } k \ne 0 \end{cases} \end{align*} \]

我们已经多次强调，当一个模型很好的捕捉了原始时间序列的自相关性，它的残差序列就应该没有任何（统计意义上显著的）自相关性了。换句话说，一个优秀模型的残差序列应该（近似）为一个白噪声。因此，使用白噪声序列的性质可以帮助我们确认我们的残差序列中没有任何相关性了，一旦残差序列没有相关性便意味着模型是原始时间序列的一个良好的拟合。

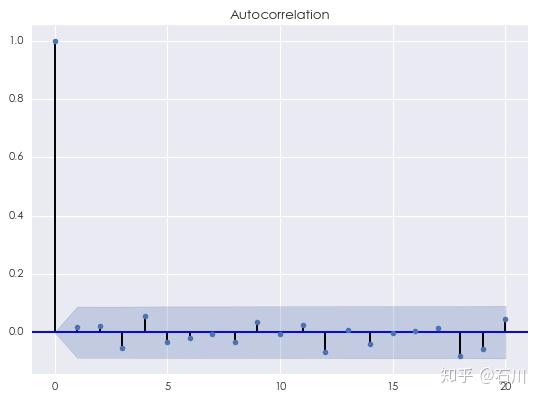
在白噪声模型中，唯一的参数就是方差$\sigma^2$。这个参数可以通过历史数据估计得到。在本系列的第一篇文章中，我们曾给出了一个白噪声序列的相关图（如下），该序列由标准正态分布生成（因此为高斯白噪声），共 500 个观测值。可以看到，对图中显示的间隔 $k$ 的取值，对所有 $k \ge 1 $ 均有自相关系数在统计上等于 $0$ 。

4 随机游走¶

将白噪声模型进行一步延伸，便得到随机游走（random walk）模型，它的定义如下：

对于时间序列${x_t}$，如果它满足 $x_t = x_{t-1} + w_t$，其中 $w_t$ 是一个均值0、方差为 $\sigma^2$ 的白噪声，则序列 $\{x_t\}$ 为一个随机游走。

由定义可知，在任意 $t$ 时刻的 $x_t$ 都是不超过 $t$ 时刻的所有历史白噪声序列的总和，即：

\[ x_t = w_t + w_{t-1} + w_{t-2} + \cdots + w_0 \]

随机游走的序列均值和方差为：

\[ \begin{align*} \mu_{x_t} & = 0 \\ Var(x_t) & = Var(w_t) + Var(w_{t-1}) + \cdots + Var(w_0) \\ & = t \times Var(w_t) \\ & = t \sigma^2 \end{align*} \]

虽然均值不随时间 $t$ 改变，但是由于方差是 $t$ 的函数，因此随机游走不满足稳定性。随着 $t$ 的增加，$x_t$ 的方差增大，说明其波动性不断增加。对于任意给定的 $k$ ，通过以下推导给得出随机游走的自协方差：

\[ \begin{align*} Cov(x_t, x_{t+k}) & = Cov(x_t, x_t + w_{t+1} + \cdots + w_k) \\ & = Cov(x_t,x_t) + \sum_{i=t+1}^{k}{Cov(x_t,w_i)} \\ & = Cov(x_t,x_t) + 0 \\ & = t\sigma^2 \end{align*} \]

上述推导中使用了独立随机变量的方差可加性。有了自协方差和方差，便可以方便的求出随机游走的自相关函数：

\[ \begin{align*} \rho_k(t) & = \frac{Cov(x_t,x_{t+k})}{\sqrt{(Var(x_t)}\sqrt{Var(x_{t+k})} } \\ & = \frac{t\sigma^2}{\sqrt{t\sigma^2}\sqrt{(t+k)\sigma^2}} \\ & = \frac{1}{\sqrt{1 + k/t}} \end{align*} \]

显然，自相关系数既是时间 $t$ 又是间隔 $k$ 的函数。 $\rho$ 的表达式说明，对于一个足够长的随机游走时间序列($t$ 很大），当考察的自相关间隔 $k$ 很小时，自相关系数近似为1。这是随机游走的一个非常重要的特性，不熟悉它往往容易造成不必要的错误。

举个例子。我们通常假设股价的对数收益率符合正态分布，因此股价对数是一个布朗运动（随机游走的一种特殊形式）。如果当前的（对数）股价是 $x_t$，由随机游走的特性可知，$t+1$ 时刻的股价的条件期望为 $E[x_{t+1}|x_t] = x_t $，即我们对下一时点的股价的最好的猜测就是当前的价格。随机游走是一个鞅（martingale）。

假如我们有一个预测股价的模型，而该模型就是用 $t$ 时刻的股价作为对 $t+1$ 时刻的股价的预测，则该模型的预测值和实际值之间的相关系数就等于股价序列的间隔为 1 的自相关系数。如果股价近似的为随机游走，那么由它的性质可知，间隔为 1 的自相关系数非常接近 1 。因此我们的股价预测模型——用今天的价格作为明天的价格的预测——的预测值和实际值之间的相关系数也非常接近 1 。这会给我们造成错觉：这个模型相当准确。

不幸的是，这个模型猜测的收益率在任何时刻都为，因此它对于我们构建交易信号毫无作用。

我看到过无数的学术论文（大多是硕士论文）中，针对投资品价格本身构建**自回归**模型。独立变量就包括历史价格，用它们和其他一些基本面或宏观经济数据来预测下一个交易日的股价。从上面的分析可知，这样的模型将会“精准的毫无用处”，因为回归模型中历史价格的系数之和将会非常接近1 。

任何价格序列的自回归模型都是耍流氓。

利用本文第三节例子中的白噪声序列，便可以构建一个人工随机游走序列的例子。它的轨迹如下图所示。

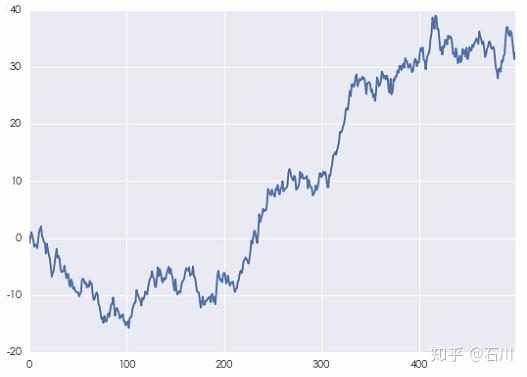
不出意外，当间隔 $k$ 相对于时间序列的长度很小时，它的自相关系数（下图）非常接近 1 ，这源自随机游走的性质。不要忘了，随机游走是对股价的对数建模。因此，这种自相关性对于基于收益率预测的投资策略并没有帮助。

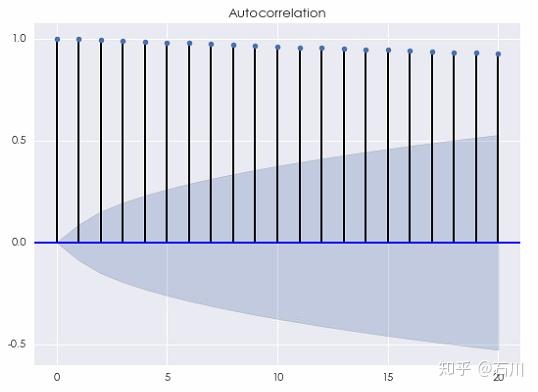
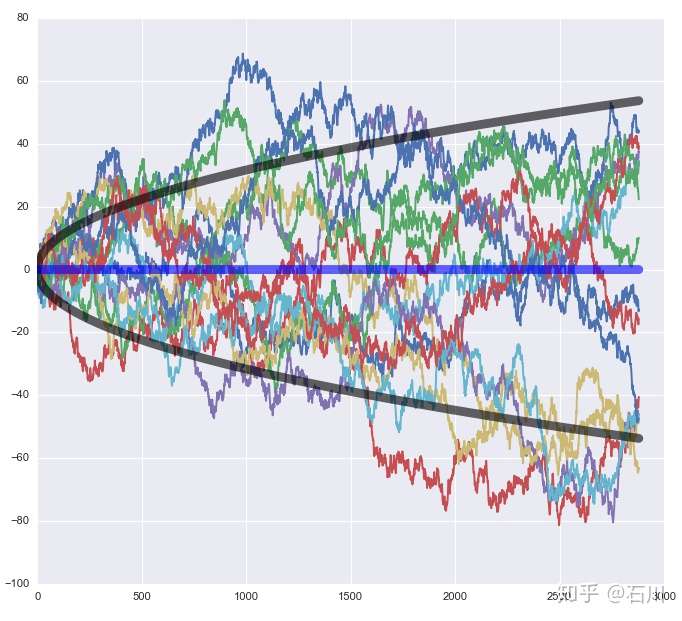
事实上，如果（对数）股价严格的符合随机游走，那么该时间序列的方差将会随时间线性增长。 这说明，长期来看它将呈现出巨大的波动。下图为来自同一个分布的 15 条随机游走的轨迹。随着时间的推进，这些轨迹上对应观测值的波动越来越大，充分的展现出随机性。

5 用白噪声对收益率建模¶

如果股票的对数收益率为白噪声，那么它的自相关系数应该在任何非零的间隔上都在统计意义上等于零。下面我们就来看看真实的股票收益率是否满足这一点。为此，考虑一支个股（万科）和一个股指（上证指数）。

以日频为例，通过交易日的复盘后收盘价可以算出对数收益率：

$r_t = lnx_t - lnx_{t-1}$

首先来看看万科，当考察期为过去 $10$ 年时，万科的对数收益率的相关图为：

上图指出，在间隔为 2 和 4 时，该收益率序列表现出了统计意义上显著的相关性。当然，由于图中的蓝色区域仅仅是 95% 的置信区间，因此仅仅根据随机性也很可能出现在一个或者两个间隔上的自相关系数处于置信区间之外的情况。因此，根据上面的结果，我们并不能一定就说白噪声不是万科收益率的一个适当的模型。

如果我们把考察的窗口缩短到过去 5 年，则万科的对数日收益率序列的相关图变为：

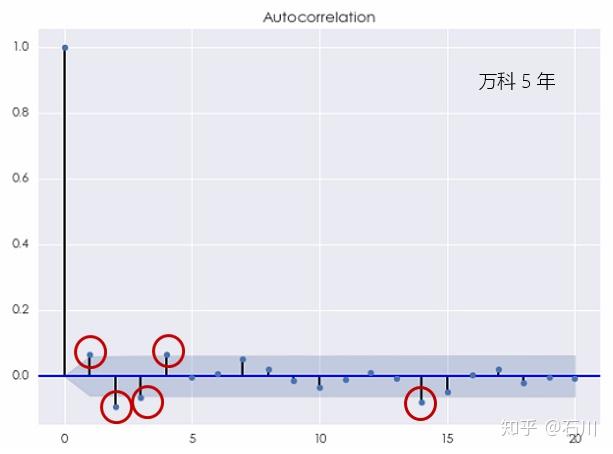
当 $k=1,2,3,4$ 以及 14 的时候，自相关系数都超过了置信区间，即在 5% 的显著性水平下不为零。**我们无法再无视这样的结果而把它们都归结于随机性。**该相关图清晰地说明白噪声不能有效的解释收益率序列中的自相关性。

对于上证指数，这种结论则更加明显。10 年还是 5 年的窗口，上证指数的对数收益率均在不同的间隔上表现出了显著的自相关（下图），且它比个股的自相关性更加显著。

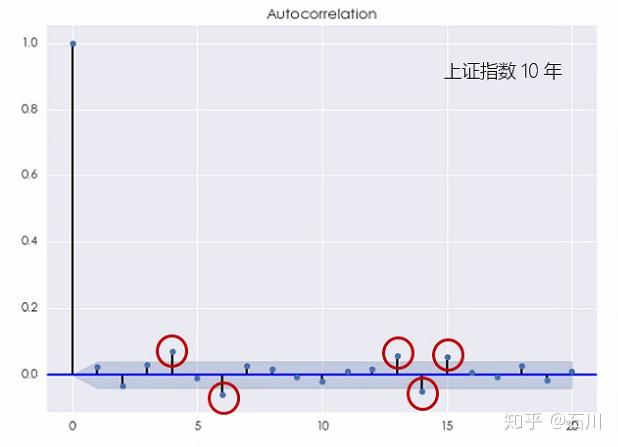
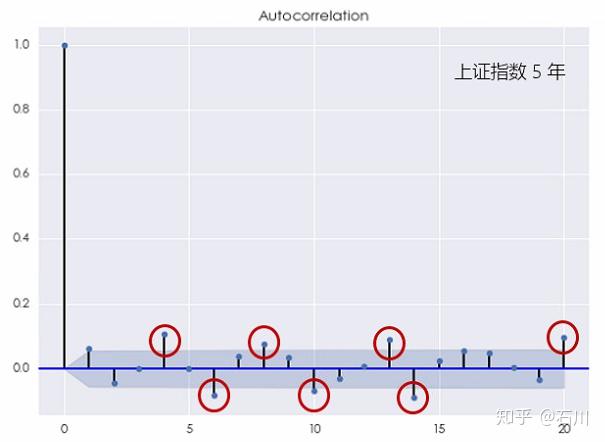
这个结果说明上证指数的对数收益率序列无法用白噪声来建模。更有意思的是，当 $k$ 较小或者较大时，上证指数的收益率均表现出了自相关性，这说明它既有短记忆又有长记忆。

6 下文预告¶

本文的分析引出如下的结论：

无论对于个股或是指数，它们的收益率序列中都存在某种自相关性，不满足白噪声模型。

因此，我们必须考虑更加高级的时间序列模型来对自相关性建模。在这方面，自回归模型（AR）和滑动平均模型（MA），以及它们二者的组合 —— 自回归滑动平均模型（ARMA） —— 都是非常有力的工具。它们将是本系列下一篇的内容。

（全文完）

免责声明： 文章内容不可视为投资意见。市场有风险，入市需谨慎。